ISO-MAG help
Table of Magnetic Space Groups
Harold T. Stokes and Branton J. Campbell, Department of Physics and Astronomy, Brigham Young University, Provo, Utah 84602, USA, branton_campbell@byu.edu
This table is based on data from:
(1) D. B. Litvin, Magnetic Group Tables (International Union of
Crystallography, 2013) www.iucr.org/publ/978-0-9553602-2-0.
(2) C. J. Bradley and A. P. Cracknell, The Mathematical Theory of
Symmetry in Solids (Clarendon Press, Oxford, 1972).
Note that in version 1.3 (Nov 2021)
of these tables, the unified (UNI) symbols for
the BNS setting were added. For a detailed description of the UNI symbols,
see:
B. J. Campbell, H. T. Stokes, J. M. Perez-Mato and J. Rodriguez-Carvajal,
"Introducing a Unified Magnetic Space-Group Symbol,"
Acta Cryst. A78 99-106 (2022).
Types of Magnetic Space Groups
The 1651 Shubnikov/Heesch magnetic space groups combine the 230 crystallographic space groups with the time reversal operator. We denote space-group operators as (p|t), where p is a point operator and t is a translation. The time reversal operator is expressed as (1|0,0,0)' or 1'. To make our descriptions more intuitive, we occasionally refer to a symmetry operation as "primed" or "black" if it includes "time reversal", or refer to it as "unprimed" or "white" if it does not. Thus, a primed operator like (p|t)' is understood to include time reversal.
Each magnetic space group G is classified as one of four different types depending on how it is constructed from the one of the 230 crystallographic space groups F:
(1) G = F (Federov groups). For this type, no operator contains time reversal. The magnetic space group symbol is the same as that for the corresponding crystallographic space group.
(2) G = F + F1'. The magnetic space group symbol ends in 1' because the pure time reversal (1|000)' is an operator in the group. The magnetic group contains two copies of every spatial operator, one with a time reversal and one without. Because each operator is both black and white, we call this a "grey" group. A grey group can describe a paramagnetic material in zero external magnetic field -- the average magnetic moment of every atom is zero.
(3) G = D + (F - D)1', where D is an equi-translational subgroup of F of index 2. Each operator of a type-3 magnetic space group is either black or white, so that exactly half of the point operators include a time reversal. We thus say that a type-3 magnetic space group has a "colored" point group. The lattice translations, however, do not include time-reversal. In the magnetic space-group symbol, the generators of the magnetic point group that include a time reversal are indicated by the prime symbol.
(4) G = D + (F - D)1', where D is an equi-class subgroup of F of index 2. Each translational symmetry of the magnetic lattice is either black or white, so that exactly half of the lattice translations include time reversal. We thus say that a type-4 magnetic space group has a "colored" lattice. After the translations and point symmetries are combined, each point operator appears both with and without a time-reversal, so that the magnetic point group of a type-4 magnetic space group is actually a grey group. The magnetic space-group symbol adds a subscript to the leading letter (i.e. the lattice indicator) to indicate the magnetic lattice type. In some cases (described below), a type-4 group symbol will also have primes on some of the point-group generators.
Settings
Historically, the magnetic space groups have been classified using two different settings:
BNS: N. V. Belov, N. N. Neronova and T. S. Smirnova
OG: W. Opechowski and R. Guccione
The BNS and OG settings and symbols are identical for type-1, type-2 and type-3 groups, and are derived from subgroup F described above.
For type-4 groups, however, the BNS setting and symbols are derived from D, while the OG setting and symbols are derived from F. In G, pure lattice translations such as (1|u) are contained in D, while lattice translations with time reversal such as (1|v)' are contained in (F-D)1'. Both u and v are lattice translations in F, but only u is a lattice translation in D. Therefore, in the BNS setting, operators containing 1' are accompanied only by fractional translations, whereas in the OG setting, they are accompanied by integral lattice translations. For example, consider BNS:67.509 Camma and OG:47.11.357 PCmmm', which are the same group. In this case, F=Pmmm and D=Cmma. BNS bases its symbol Camma on D=Cmma (#67), while OG bases its symbol PCmmm' on F=Pmmm (#47). The BNS setting contains the operator (1|1/2,0,0)', while the OG setting expresses the same operator as (1|0,1,0)'.
We refer to the BNS and OG descriptions of a given magnetic structure as two different "settings" of the same magnetic symmetry because there always exists an affine transformation matrix that allows one to transform the structural details (lattice vectors, atomic coordinates, magnetic moments, thermal parameters, etc.) back and forth between the two descriptions. This procedure puts the transformation between the BNS and OG settings on par with other common setting changes such as axes permutations, origin shifts and centering transformations.
BNS Lattice Symbols for Type-4
For type-4 groups in the BNS setting, the magnetic space-group symbol is the crystallographic space-group symbol for D with a subscript added to the first letter, denoting the type of colored lattice. The BNS lattice is defined only by the white points, which are the lattice points t of D. The black points are at t+v, where v is a fractional translation. Below we define the symbols for the colored lattices by giving the fractional v.
| Symbol | Fractional |
| PS | (0,0,1/2) triclinic only |
| Pa | (1/2,0,0) |
| Pb | (0,1/2,0) |
| Pc | (0,0,1/2) |
| PA | (0,1/2,1/2) |
| PB | (1/2,0,1/2) |
| PC | (1/2,1/2,0) |
| PI | (1/2,1/2,1/2) |
| Aa | (1/2,0,0) |
| Ab | (0,1/2,0) |
| AB | (1/2,0,1/2) |
| Bb | (0,1/2,0) |
| Ba | (1/2,0,0) |
| BA | (0,1/2,1/2) |
| Cc | (0,0,1/2) |
| Ca | (1/2,0,0) |
| CA | (0,1/2,1/2) |
| FS | (1/2,1/2,1/2) |
| Ia | (1/2,0,0) |
| Ib | (0,1/2,0) |
| Ic | (0,0,1/2) |
| RI | (0,0,1/2) |
OG Lattice Symbols for Type-4
For type-4 groups in the OG setting, the magnetic space-group symbol is the crystallographic space-group symbol for F with a subscript added to the first letter, denoting the type of colored lattice. In the OG setting, the lattice of F is decorated by both black and white points, so that the white points form a sublattice of F. Below we define the symbols for each colored lattice by giving the basis vectors of the corresponding primitive sublattice.
| Symbol | Sublattice |
| P2s | (1,0,0,),(0,1,0),(0,0,2) triclinic only |
| P2a | (2,0,0,),(0,1,0),(0,0,1) |
| P2b | (1,0,0),(0,2,0),(0,0,1) |
| P2c | (1,0,0),(0,1,0),(0,0,2) |
| PA | (1,0,0),(0,1,1),(0,-1,1) |
| PB | (1,0,1),(0,1,0),(-1,0,1) |
| PC | (1,1,0),(-1,1,0),(0,0,1) non-tetragonal only |
| PP | (1,1,0),(-1,1,0),(0,0,1) tetragonal only |
| PF | (0,1,1),(1,0,1),(1,1,0) non-tetragonal only |
| PI | (0,1,1),(1,0,1),(1,1,0) tetragonal only |
| A2a | (2,0,0),(0,1/2,1/2),(0,-1/2,1/2) |
| AP | (1,0,0),(0,1,0),(0,0,1) |
| AI | (1,1/2,1/2),(0,1,0),(0,0,1) |
| B2b | (1/2,0,1/2),(0,2,0),(-1/2,0,1/2) |
| BP | (1,0,0),(0,1,0),(0,0,1) |
| BI | (1,0,0),(1/2,1,1/2),(0,0,1) |
| C2c | (1/2,1/2,0),(-1/2,1/2,0),(0,0,2) |
| CP | (1,0,0),(0,1,0),(0,0,1) |
| CI | (1,0,0),(0,1,0),(1/2,1/2,1) |
| FA | (1,0,0),(0,1/2,1/2),(0,-1/2,1/2) |
| FB | (1/2,0,1/2),(0,1,0),(-1/2,0,1/2) |
| FC | (1/2,1/2,0),(-1/2,1/2,0),(0,0,1) |
| IP | (1,0,0),(0,1,0),(0,0,1) |
| IA | (1/2,1/2,1/2),(0,1,1),(0,-1,1) |
| IB | (1,0,1),(1/2,1/2,1/2),(-1,0,1) |
| IC | (1,1,0),(-1,1,0),(1/2,1/2,1/2) |
| RR | (1/3,2/3,2/3),(-2/3,-1/3,2/3),(1/3,-1/3,2/3) |
BNS Magnetic Space-Group Symbols for Type-4
Start with the space group symbol of subgroup D, and simply modify the lattice symbol to indicate the correct BNS magnetic lattice. No primes are added to the point-group generator symbols because each point operator is both black and white (i.e. grey).OG Magnetic Space-Group Symbols for Type-4
Start with the space group symbol of non-magnetic subgroup F, and modify the lattice symbol to indicate the correct OG magnetic lattice. In contrast to the BNS symbols for type-4 magnetic space groups, primes must then be added to the point-group generators of a type-4 OG symbol in order to distinguish between different magnetic space groups with the same type of magnetic OG lattice. To determine which generators should receive a prime, OG define one representative operator for each kind of point operator in F. (In technical terms, these are coset representatives of F with respect to its translation group.) The placement of these primes is arbitrary in principle. Because the placements selected by OG now comprise a historical standard, it is helpful to know that they were based on the lists of representative operators explicitly given in Vol. 1 of the 1952 edition of International Tables for X-Ray Crystallography (ITC52, origin choice 1 when more than one origin choice is given).For example, the representative operators in ITC52 for 49 Pccm are chosen to be (1|0,0,0), (2x|0,0,1/2), (2y|0,0,1/2), (2z|0,0,0), (-1|0,0,0), (mx|0,0,1/2), (my|0,0,1/2), (mz|0,0,0). The consecutive symbols c,c,m in Pccm refer to the generators (mx|0,0,1/2), (my|0,0,1/2), (mz|0,0,0), respectively. The magnetic space groups based on F=Pccm and the P2a lattice are listed below. In each case, the presence of absence of time reversal on each of these generators determines the OG symbol.
| Symbol | Generators |
| 49.8.371 P2accm | (mx|0,0,1/2),(my|0,0,1/2),(mz|0,0,0) |
| 49.10.373 P2accm' | (mx|0,0,1/2),(my|0,0,1/2),(mz|0,0,0)' |
| 49.11.374 P2ac'c'm | (mx|0,0,1/2)',(my|0,0,1/2)',(mz|0,0,0) |
| 49.12.375 P2ac'c'm' | (mx|0,0,1/2)',(my|0,0,1/2)',(mz|0,0,0)' |
As another example, the representative operators for 24 I212121 are listed as (1|0,0,0), (2x|1/2,1/2,0), (2y|0,1/2,1/2,), (2z|1/2,0,1/2) in ITC52. The consecutive symbols 21,21,21 in I212121 refer to the generators (2x|1/2,1/2,0), (2y|0,1/2,1/2,), (2z|1/2,0,1/2), respectively. The magnetic space groups based on F=I212121 and the IP lattice are as follows:
| Symbol | Generators |
| 24.4.153 IP212121 | (2x|1/2,1/2,0),(2y|0,1/2,1/2),(2z|1/2,0,1/2) |
| 24.5.154 IP21'21'21 | (2x|1/2,1/2,0)',(2y|0,1/2,1/2)',(2z|1/2,0,1/2) |
Note that we could have just as well ignored ITC52 and chosen the representative operators for 24 I212121 to be (1|0,0,0), (2x|0,0,1/2), (2y|1/2,0,0), (2z|0,1/2,0). In that case the symbols would have been 24.4.153 IP21'21'21' and 24.5.154 IP212121'. It is not obvious by inspection which operators are to be primed. Only by relying on the operators explicitly given in ITC52 can we see how the primes were placed by OG.
Changes to the form of the representative operators listed in subsequent versions of the International Tables of Crystallography (ITC) have led to some confusion (Litvin).
The strict use of ITC52 operators is not always sufficient for determining the OG symbol. For example, the representative operators for 93 P4222 are chosen to be (1|0,0,0), (4z|0,0,1/2), (4z-1|0,0,1/2), (2x|0,0,0), (2y|0,0,0), (2z|0,0,0), (2xy|0,0,1/2), (2-xy|0,0,1/2) in ITC52. For this space group symbol, the consecutive point-operator symbols {42,2,2} refer to sets of related operators: {(4z|0,0,1/2), (4z-1|0,0,1/2)}, {(2x|0,0,0), (2y|0,0,0)}, and {(2xy|0,0,1/2), (2-xy|0,0,1/2)}, rather than to individual operators. Usually, when one operator in such a set contains time reversal, all of the operators in that set do. But this is not always the case. For 93.6.781 P2c4222', (2y|0,0,0)' has the time reversal while (2x|0,0,0) does not. This leaves us with an arbitrary decision to make: should we prime the corresponding 2 in the symbol or not? In 2011, Litvin recommended that this ambiguity be resolved by using the representative operator associated with a given generator symbol from the table, Representatives for the sets of lattice symmetry directions in the various crystal families, Chapter 12, "Space-Group Symbols and Their Use," by H. Burzlaff and H. Zimmerman, in ITC, Vol. A. (Note that the table number is different in various editions of ITC.) For the cases of interest here, that table gives the following representative operators:
| Point Group | Operators |
| 422 | 4z, 2x, 2-xy |
| 321 | 3z, 2x, 1 |
| 312 | 3z, 1, 23 |
| 622 | 6z, 2x, 23 |
| m-3 | -2z, -3xyz |
The following table lists all of the magnetic space groups for which sets of related operators contain the time reversal and some do not. Though OG did not use the above-convention in treating these groups historically, we have followed Litvin by applying the new convention here in all but two cases (153.4.1270 and 154.4.1274 -- see discussion below), which changed the OG symbols for seven of the magnetic space groups (only the new symbols are shown here).
| Group | Operators |
| 93.6.781 P2c4222' | {(2x|0,0,0),(2y|0,0,0)'} & {(2xy|0,0,1/2),(2-xy|0,0,1/2)'} |
| 93.8.783 PI4222' | {(2x|0,0,0),(2y|0,0,0)' & {(2xy|0,0,1/2),(2-xy|0,0,1/2)'} |
| 93.9.784 P2c42'22 | {(2x|0,0,0),(2y|0,0,0)'} & {(2xy|0,0,1/2)',(2-xy|0,0,1/2)} |
| 94.6.791 P2c42212 | {(2x|1/2,1/2,1/2),(2y|1/2,1/2,1/2)'} & {(2xy|0,0,0)',(2-xy|0,0,0)} |
| 94.7.792 P2c42'21'2 | {(2x|1/2,1/2,1/2)',(2y|1/2,1/2,1/2)} & {(2xy|0,0,0)',(2-xy|0,0,0)} |
| 98.6.819 IP4122 | {(2x|0,1/2,1/4),(2y|0,1/2,1/4)'} & {(2xy|0,0,0)',(2-xy|0,0,0)} |
| 98.7.820 IP41'22' | {(2x|0,1/2,1/4),(2y|0,1/2,1/4)'} & {(2xy|0,0,0),(2-xy|0,0,0)'} |
| 98.8.821 IP412'2' | {(2x|0,1/2,1/4)',(2y|0,1/2,1/4)} & {(2xy|0,0,0),(2-xy|0,0,0)'} |
| 98.9.822 IP41'2'2 | {(2x|0,1/2,1/4)',(2y|0,1/2,1/4)} & {(2xy|0,0,0)',(2-xy|0,0,0)} |
| 151.4.1262 P2c3212 | {(21|0,0,0),(22|0,0,1/3)',(23|0,0,2/3)} |
| 152.4.1266 P2c3221 | {(2x|0,0,2/3),(2xy|0,0,0),(2y|0,0,1/3)'} |
| 153.4.1270 P2c3112 | {(21|0,0,0),(22|0,0,2/3),(23|0,0,1/3)'} |
| 154.4.1274 P2c3121 | {(2x|0,0,1/3)',(2xy|0,0,0),(2y|0,0,2/3)} |
| 180.6.1401 P2c6222' | {(2x|0,0,0),(2xy|0,0,2/3),(2y|0,0,1/3)'} |
| & {(21|0,0,1/3),(22|0,0,0)',(23|0,0,2/3)'} | |
| 180.7.1402 P2c62'22 | {(2x|0,0,0),(2xy|0,0,2/3),(2y|0,0,1/3)'} |
| & {(21|0,0,1/3)',(22|0,0,0),(23|0,0,2/3)} | |
| 181.6.1408 P2c6422' | {(2x|0,0,0),(2xy|0,0,1/3)',(2y|0,0,2/3)} |
| & {(21|0,0,2/3),(22|0,0,0),(23|0,0,1/3)'} | |
| 181.7.1409 P2c64'2'2' | {(2x|0,0,0)',(2xy|0,0,1/3),(2y|0,0,2/3)'} |
| & {(21|0,0,2/3),(22|0,0,0),(23|0,0,1/3)'} | |
| 206.4.1541 IPa-3' | {(-3xyz|0,0,0)',(-3xyz-1|0,0,0)',(-3-xyz|1/2,0,0),(-3-xyz-1|0,1/2,0), |
| (-3x-yz|0,1/2,0),(-3x-yz-1|0,0,1/2),(-3xy-z|0,0,1/2),(-3xy-z-1|1/2,0,0)} |
Finally, there are some cases (see list below) where the OG symbol is based on the symbol for D instead of F. Two of these groups (153.4.1270 and 154.4.1274) were also mentioned in the previous paragraph. We propose that at some future time, the symbols for these six groups be brought into compliance with the conventions above: (1) base the OG symbol on F, and (2) use primes when the representative generator contains time reversal.
| Group | F | D |
| 144.3.1236 P2c32 | P31 | P32 |
| 145.3.1239 P2c31 | P32 | P31 |
| 151.4.1262 P2c3212 | P3112 | P3212 |
| 152.4.1266 P2c3221 | P3121 | P3221 |
| 153.4.1270 P2c3112 | P3212 | P3112 |
| 154.4.1274 P2c3121 | P3221 | P3121 |
We propose that at some future time, the symbols for these six groups be brought into compliance with convention: base the symbol on F and use primes in cases where the representative generator contains time reversal:
| Proposed Symbols |
| 144.3.1236 P2c31 |
| 145.3.1239 P2c32 |
| 151.4.1262 P2c3112 |
| 152.4.1266 P2c3121 |
| 153.4.1270 P2c3212' |
| 154.4.1274 P2c322'1 |
Explanation of the Table
There are two tables. In Table 1, each of the 1651 magnetic space groups are listed in order of their BNS numbers. In Table 2, each of the 1651 magnetic space groups are listed in order of their OG numbers. For each group, we include the following information.
(a) Number and symbol, given in both the BNS and OG settings. The symbols are identical except for type-4 groups.
(b) OG-BNS transformation for each type-4 group.. We give the origin and axes of the subgroup D with respect to F. These transformations are from Litvin, though we do make some adjustments to his transformations for space groups which have two origin choices: Litvin uses origin choice 1, while we use origin choice 2. We give the origin and axes of the subgroup D with respect to F. The corresponding 4x4 affine transformation matrix is easily constructed. For example, if the transformation is given as (1/4,0,0;b,c,a), the affine transformation matrix T would be
| 0 | 0 | 1 | 1/4 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 |
If gBNS and gOG are operators in the BNS and OG settings, respectively, then
gOG = T gBNS T-1.
(c) Operators. The operators are listed using symbols from Litvin. The operators follow the conventions in ITC using monoclinic unique axis b, monoclinic cell choice 1, hexagonal axes for trigonal groups, and origin choice 2 for groups with more than one origin choice. For type-4 magnetic space groups, the same operators are expressed in both the BNS and OG settings. This requires the number of OG operators to be double the number associated with subgroup F so as to fill an orbit that spans the entire magnetic repeating unit.
(d) Wyckoff sites. The x,y,z positional coordinates and the mx,my,mz components of magnetic moment are listed for each symmetry-equivalent site of each Wyckoff orbit. The classification of Wyckoff sites depends only on the action of group operators on the x,y,z coordinates. Time reversal only affects the allowed magnetic moments at each site and does not affect the x,y,z coordinates. If we remove time reversal from every operator in G, we obtain subgroup F. Therefore the Wyckoff sites for G are the same as those for F.
For type-4 magnetic space groups, the Wyckoff positions are given for both the BNS and OG settings. The positions in the two settings are related by the OG-BNS transformation described in (b) above. One must be cautious when interpreting the Wyckoff positions of type-4 groups in the OG setting, since not all integer translations are true lattice translations that take a position to an equivalent position.
For example, the transformation between BNS:72.547 Ibbam and OG:67.10.586 CImma is given by (0,0,0;b,2c,a). In Ibbam, equivalent Wyckoff positions are obtained by adding any integers to the x, y, or z coordinates or by adding the centering translation (1/2,1/2,1/2). In CImma, equivalent Wyckoff positions are obtained by adding any integer to the x or y coordinates, any even integer to the z coordinate, and by adding the "centering" translation (1/2,1/2,1). In contrast, adding an odd integer to the z component does not take us to an equivalent Wyckoff position in the OG setting because that operation in CImma includes time reversal. In the table, we list a generating set (not necessarily minimal) of lattice translations in both the BNS and OG settings. For this example, we list (0,0,0)+ (1/2,1/2,1/2)+ in the BNS setting, and (0,0,0)+ (0,1,0)+ (0,0,2)+ (1,0,0)+ (1/2,1/2,1)+ in the OG setting.
Symbols for Alternative Magnetic Space-Group Settings
The ITC lists alternate settings for many of the 230 crystallographic space groups. Besides the various settings illustrated in the detailed description of each space group, ITC also lists additional settings in Table 4.3.1, "Index of symbols of space groups for various settings and cells". Because the symbol of every magnetic space group is derived from the symbol of a non-magnetic space group, the same alternative settings apply to magnetic space groups as well. Here, we describe how the BNS and OG symbols of a magnetic space group can be determined for a variety of alternative settings. The transformation of a magnetic space-group symbol from one setting to another can be accomplished in three steps. First, transform the non-magnetic symbol from which the magnetic symbol was derived. Second, for transformations that permute or rename the principal crystal directions, let the prime associated with a given generator in the point-group symbol follow that generator through the transformation. Third, for type-4 magnetic space groups, modify the lattice symbol to represent the appropriate black-and-white lattice.We note that changing the origin of a space group does not change its symbol. Also, for trigonal groups, the symbol is the same whether rhombohedral or hexagonal axes are used.
Monoclinic settings: Six different permutations of the axes are possible: a(b)c, c(-b)a, ab(c), ba(-c), (a)bc, (-a)cb. ITC also gives three different cell choices. For each of these settings, the primes in the magnetic space group symbol follow the generators to which they were originally attached. The symbols C2/m', A2/m', B2/m', I2/m' all refer to different settings of BNS 12.61 = OG 12.4.69. Observe that the prime stays with the m generator rather than jumping to the 2 generator. As another example, P2/c', P2/a', P2/b', P2/n' all refer to different settings of BNS 13.68 = OG 13.4.80. In each case, the prime always occurs on the symbol for the glide plane, even though it has different labels in different settings.
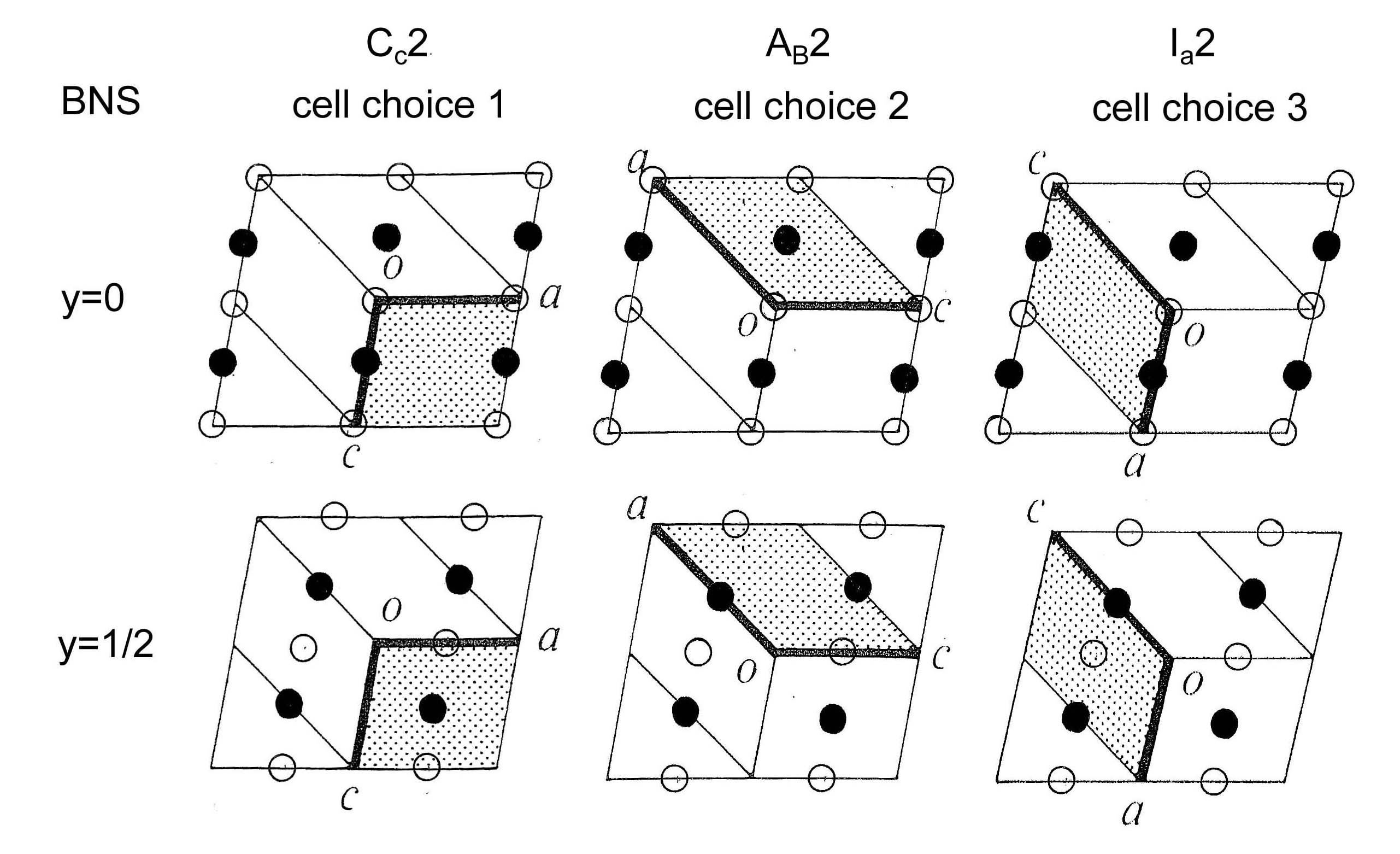
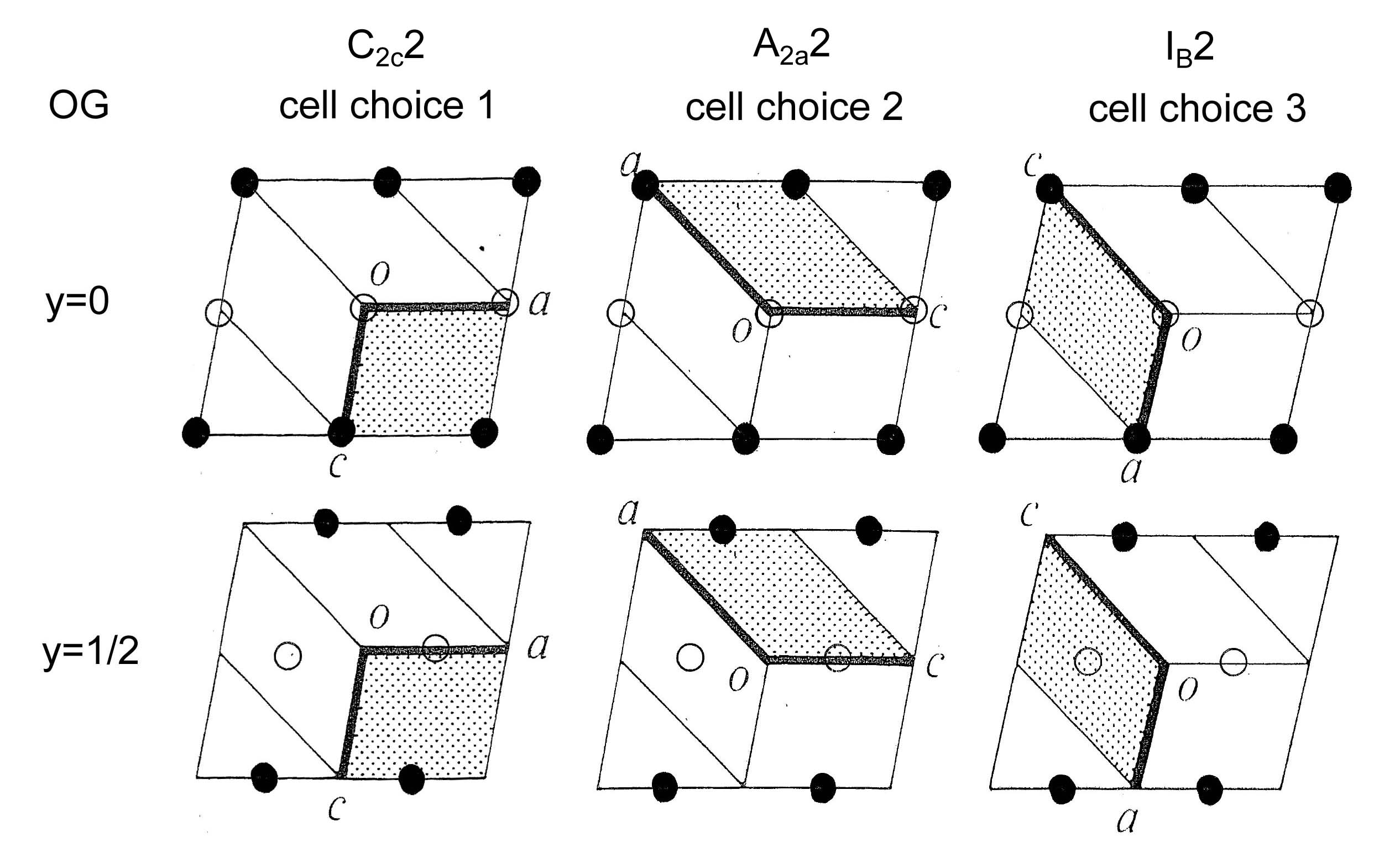
Now consider magnetic space group BNS 5.16 Cc2 = OG 5.4.22 C2c2, which requires considerably more care due to its colored lattice. F and D are different subgroups of G here, but both have the same space-group type (#5 C2), which makes the BNS and OG symbols look more similar that they might otherwise be. This should make the details of this example easier to appreciate. In the figures below, open circles ("white points") represent translations without time reversal, and the filled circles ("black points") represent translations with time reversal.
BNS setting. The figure below illustrates the colored lattice and the BNS cell of this space group for each of the three monoclinic cell choices and special-axis b. For cell choice 1, the white lattice is C-centered, and the black point at (0,0,1/2) yields BNS magnetic lattice Cc, so that the magnetic space-group symbol is Cc2. For cell choice 2, the white lattice is B-centered and the black point is at (1/2,0,1/2), so that the symbol is AB2. For cell choice 3, the white lattice is body centered and the black point is at (1/2,0,0), so that the symbol is Ia2.
OG setting: The figure below illustrates the colored lattice and the OG cell of this space group for each of the three monoclinic cell choices and special-axis b.. Observe that the OG "unit cell" has half the volume of the BNS cell and has both black and white corners. For cell choice 1, the basis vectors of the white sublattice relative to those of the combined black-white lattice are (1/2,1/2,0), (-1/2,1/2,0), (0,0,2), yielding magnetic lattice C2c and magnetic space-group symbol C2c2. For cell choice 2, the basis vectors are (2,0,0), (0,1/2,1/2), (0,-1/2,1/2), and the symbol for the magnetic space group is A2a2. For cell choice 3, the basis vectors are (1,0,1), (1/2,1/2,1/2), (-1,0,1) and the symbol for the magnetic space group is IB2. Note that the IB colored lattice occurs only for centered monoclinic settings and cell-choice-3, and is therefore not listed by Litvin.
Orthorhombic settings: Six different permutations of the axes are possible: abc, ba-c, cab, -cba, bca, a-cb. Primes in the magnetic space group symbol follow the generators they are attached to. For example, Pnma', Pmnb', Pb'nm, Pc'mn, Pmc'n, Pna'm all refer to different settings of BNS 62.445 = OG 62.5.506. For type-4 groups, the letters in the subscript denoting the magnetic lattice must be permuted as well. For example, P2cm'mn, P2cmm'n,P2anm'm,P2anmm',P2bmnm', P2bm'nm all refer to different settings of OG 59.9.486.
OG-BNS Transformation Example
From the table:
BNS: 80.32 I_c4_1 OG: 77.6.677 P_I4_2
OG-BNS transformation: (0,1/2,0;a-b,a+b,2c)
Operators (BNS): (1|0,0,0) (4z|0,1/2,1/4) (4z-1|1/2,0,3/4) (2z|1/2,1/2,1/2)
(1|0,0,1/2)' (4z|0,1/2,3/4)' (4z-1|1/2,0,1/4)' (2z|1/2,1/2,0)'
Wyckoff positions (BNS): (0,0,0)+ (1/2,1/2,1/2)+
16d (x,y,z;mx,my,mz) (-y,x+1/2,z+1/4;-my,mx,mz) (y+1/2,-x,z+3/4;my,-mx,mz)
(-x+1/2,-y+1/2,z+1/2;-mx,-my,mz) (x,y,z+1/2;-mx,-my,-mz)
(-y,x+1/2,z+3/4;my,-mx,-mz) (y+1/2,-x,z+1/4;-my,mx,-mz)
(-x+1/2,-y+1/2,z;mx,my,-mz)
8c (0,0,z;0,0,mz) (0,1/2,z+1/4;0,0,mz) (0,0,z+1/2;0,0,-mz) (0,1/2,z+3/4;0,0,-mz)
8b (1/4,1/4,z;mx,my,0) (3/4,3/4,z+1/4;-my,mx,0) (3/4,3/4,z+3/4;my,-mx,0)
(1/4,1/4,z+1/2;-mx,-my,0)
8a (1/4,3/4,z;mx,my,0) (1/4,3/4,z+1/4;-my,mx,0) (1/4,3/4,z+3/4;my,-mx,0)
(1/4,3/4,z+1/2;-mx,-my,0)
Operators (OG): (1|0,0,0) (4z|0,0,1/2) (4z-1|0,0,3/2) (2z|0,0,1) (1|0,0,1)'
(4z|0,0,3/2)' (4z-1|0,0,1/2)' (2z|0,0,0)'
Wyckoff positions (OG): (0,0,0)+ (1,-1,0)+ (1,1,0)+ (0,0,2)+ (1,0,1)+
16d (x,y,z;mx,my,mz) (-y,x,z+1/2;-my,mx,mz) (y,-x,z+3/2;my,-mx,mz)
(-x,-y,z+1;-mx,-my,mz) (x,y,z+1;-mx,-my,-mz) (-y,x,z+3/2;my,-mx,-mz)
(y,-x,z+1/2;-my,mx,-mz) (-x,-y,z;mx,my,-mz)
8c (0,1/2,z;0,0,mz) (-1/2,0,z+1/2;0,0,mz) (0,1/2,z+1;0,0,-mz)
(-1/2,0,z+3/2;0,0,-mz)
8b (1/2,1/2,z;mx,my,0) (-1/2,1/2,z+1/2;-my,mx,0) (1/2,-1/2,z+3/2;my,-mx,0)
(-1/2,-1/2,z+1;-mx,-my,0)
8a (0,0,z;mx,my,0) (0,0,z+1/2;-my,mx,0) (0,0,z+3/2;my,-mx,0) (0,0,z+1;-mx,-my,0)
From the OG-BNS transformation, (0,1/2,0;a-b,a+b,2c),
we obtain the affine transformation matrix: T =
((1,1,0,0),(-1,1,0,1/2),(0,0,2,0),(0,0,0,1)).
Because gOG = T gBNS T-1, we also know
that gBNS = T-1 gOG T .
The point portion of the transformation is matrix TP =
((1,1,0),(-1,1,0),(0,0,2)).
The purely rotational component of TP is TR =
((0.707,0.707,0),(-0.707,0.707,0),(0,0,1)).
Let the OG description of a two-atom structure be as follows:
OG: 77.6.677 PI42
Cell parameters: a = 2.5 Å, c = 3.0 Å
A: 16d (x,y,z) = (0.1, 0.2, 0.3); (mx,my,mz) = (1.414, 1.414, 0)μB;
(u11,u22,u33,u12,u13,u23) = (0.11, 0.22, 0.33, 0.12, 0.13, 0.23)
B: 8c (0,1/2,z) = (0, 1/2, 0.4); (0,0,mz) = (0, 0, 1.5)μB;
(u11,u11,u33,u12,0,0) = (0.11, 0.22, 0.33, 0.12, 0, 0)
The lattice of the OG cell can be described by a matrix of three
column vectors (a | b | c),
BOG = ((2.5,0,0),(0,2.5,0),(0,0,3.0)), which transforms as
BBNS = BOG T3D = ((2.5,2.5,0),(-2.5,2.5,0),(0,0,6.0)).
This corresponds to a tetragonal lattice with a = 3.54 Å, c = 6.0 Å.
The first atom position transforms as xBNS = T-1 xOG = T-1 (0.1,
0.2, 0.3, [1]) = (0.2, -0.1, 0.15, [1])
The corresponding moment transforms as mBNS =
TR-1 mOG =
TR-1 (1.414, 1.414, 0) = (0, 2.0, 0)
The corresponding thermal ellipsoid transforms as uBNS = TR-1 uOG TR
= TR-1 ((0.11,0.12,0.13),
(0.12,0.22,0.23), (0.13,0.23,0.33)) TR
= ((0.045, -0.055, -0.071), (-0.055, 0.285, 0.255), (-0.071,
0.255, 0.33)
The second atom position transforms as xBNS =
T-1 xOG = T-1 (0, 1/2, 0.4, [1]) =
(0, 0, 0.2, [1])
The corresponding moment transforms as mBNS =
TR-1 mOG =
TR-1 (0, 0, 1.5) = (0, 0, 1.5)
The corresponding thermal ellipsoid transforms as uBNS
= TR-1 uOG TR
= TR-1 ((0.11, 0.12, 0),(0.12, 0.22, 0),(0,
0, 0.33)) TR
= ((0.045,-0.055,0), (-0.055, 0.285, 0), (0, 0, 0.33))
Thus, the BNS description of this two-atom structure is as follows:
BNS: 80.32 Ic41
Cell parameters: a = 3.54 Å, c = 6.0 Å
A: 16d (x,y,z) = (0.2, -0.1, 0.15); (mx,my,mz) = (0, 2.0, 0)μB;
(u11,u22,u33,u12,u13,u23) = (0.045, 0.285, 0.33, -0.055, -0.071, 0.255)
B: 8c (0,0,z) = (0, 1/2, 0.4); (0,0,mz) = (0, 0, 1.5)μB;
(u11,u11,u33,u12,0,0) = (0.045, 0.285, 0.33, -0.055, 0, 0)
The direction of the transform can just as easily be reversed to recover the OG description.
Because the moments are defined as projections along the crystal
axes, they need to be transformed into cartesian coordinates in order
to determine their magnitudes. For this purpose, we define a matrix L
= ((a,0,0),(0,b,0),(0,0,c)), which unlike B, is always a diagonal
matrix containing the three cell edge lengths. In this simple
orthorhombic example, B and L are identical. The magnitudes of the
moments, which are invariant with respect to setting, are computed as
|M| = |BOG LOG-1 mOG|
= |(1.414, 1.414, 0)|
= |BBNS LBNS-1 mBNS|
= |(0, 2.0, 0)| = 2.0 μB for the 1st atom, and
|M| = |BOG LOG-1 mOG|
= |(0, 0, 1.5)|
= |BBNS LBNS-1 mBNS|
= |(0, 0, 1.5)| = 1.5 μB for the 2nd atom.
Corrections
July 2013
In July 2013, we discovered an error in the BNS symbols for eight of the
magnetic space groups:
227.130 Fd'-3m should be Fd'-3'm,
227.132 Fd'-3m' should be Fd'-3'm',
228.136 Fd'-3c should be Fd'-3'c,
228.138 Fd'-3c' should be Fd'-3'c',
229.142 Im'-3m should be Im'-3'm,
229.144 Im'-3m' should be Im'-3'm',
230.147 Ia'-3d should be Ia'-3'd,
230.149 Ia'-3d' should be Ia'-3'd'.
These errors were introduced when we copied the symbols from Bradley and Cracknell and then changed 3 to -3 to be consistent with current symbols in International Tables of Crystallography. For example, 227.130 is listed correctly as Fd'3m in Bradley and Cracknell. We changed the symbol to Fd'-3m. However, in this space group, 3xyz is not followed by a time reversal, but -3xyz' is, so we should have put a prime on the -3 in the symbol. These symbols have now been corrected in our tables.
May 2022
In May 2022, a user alerted us about some differences between our symbols and those in Litvin and in Bradley and Cracknell.
OG symbols:
16.6.104 P_I222 should be P_F222,
25.9.163 P_Imm2 should be P_Fmm2,
34.5.235 P_Inn2 should be P_Fnn2,
47.8.354 P_Immm should be P_Fmmm,
48.6.363 P_Innn should be P_Fnnn,
153.4.1270 P_2c3_112 should be P_2c3_112',
154.4.1274 P_2c3_121 should be P_2c3_12'1.
The last two entries are due to changes Litvin made sometime before 2016.
BNS (and Unified) symbols: We did not actually make these changes
since they would then bring us into disagreement with the Bilbao
Crystallographic Server (BCS). However, we include them below for the
user's information.
18.20 P_b2_12_12 and P2_12_12.1'_b[P2_122]
should be P_a2_12_12 and P2_12_12.1'_a[P22_12],
19.28 P_c2_12_12_1 and P2_12_12_1.1'_c[P2_12_12]
should be P_a2_12_12_1 and P2_12_12_1.1'_a[P22_12_1],
18.22 P_B2_12_12 and P2_12_12.1'_B[B22_12]
should be P_A2_12_12 and P2_12_12.1'_A[A2_122],
17.13 P_B222_1 and P222_1.1'_B[B222]
should be P_A222_1 and P222_1.1'_A[A222],
38.193 A_bmm2 and Amm2.1'_b[Pmm2]
should be A_cmm2 and Amm2.1'_c[Pmm2],
39.201 A_bbm2 and Abm2.1'_b[Pmm2]
should be A_cbm2 and Abm2.1'_c[Pmm2],
40.209 A_bma2 and Ama2.1'_b[Pma2]
should be A_cma2 and Ama2.1'_c[Pma2],
32.140 P_bba2 and Pba2.1'_b[Pma2]
should be P_aba2 and Pba2.1'_a[Pbm2],
41.217 A_bba2 and Aba2.1'_b[Pma2]
should be A_cba2 and Aba2.1'_c[Pma2],
38.194 A_Bmm2 and Amm2.1'_B[Fmm2]
should be A_Cmm2 and Amm2.1'_C[Fmm2],
39.202 A_Bbm2 and Abm2.1'_B[Fmm2]
should be A_Cbm2 and Abm2.1'_C[Fmm2],
40.210 A_Bma2 and Ama2.1'_B[Fmm2]
should be A_Cma2 and Ama2.1'_C[Fmm2],
41.218 A_Bba2 and Aba2.1'_B[Fmm2]
should be A_Cba2 and Aba2.1'_C[Fmm2],
48.262 P_cnnn and Pnnn.1'_c[Pban]
should be P_annn and Pnnn.1'_a[Pncb],
59.412 P_bmmn and Pmmn.1'_b[Pmma]
should be P_ammn and Pmmn.1'_a[Pmmb],
56.372 P_bccn and Pccn.1'_b[Pcca]
should be P_accn and Pccn.1'_a[Pccb],
59.414 P_Bmmn and Pmmn.1'_B[Bmmb]
should be P_Ammn and Pmmn.1'_A[Amma],
58.402 P_Bnnm and Pnnm.1'_B[Bbmm]
should be P_Annm and Pnnm.1'_A[Amam],
74.562 I_bmma and Imma.1'_b[Bmmm]
should be I_amma and Imma.1'_a[Ammm],
49.274 P_Bccm and Pccm.1'_B[Bmcm]
should be P_Accm and Pccm.1'_A[Acmm],
72.547 I_bbam and Ibam.1'_b[Bmcm]
should be I_abam and Ibam.1'_a[Acmm].
These changes would bring our BNS symbols into agreement with Litvin, Bradley and Cracknell, and the original BNS symbols. We don't know how these differences made their way into our database. The different symbols for all but the A-centered magnetic space groups in the list represent different settings and therefore affect the space-group operations as well as the Wyckoff positions.