In this demonstration, we excite standing waves on a violin string and hear the musical pitch associated with each harmonic. This demonstration was inspired by a demonstration described by Donald E. Hall in a workshop at a national meeting of the American Association of Physics Teachers in Sacramento, California, July 2004. Also see Donald E. Hall, "Sacrificing a Cheap Guitar in the Name of Science, The Physics Teacher, Dec. 1989, p. 673.
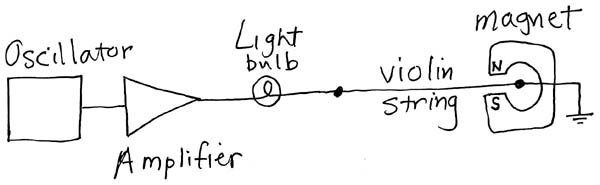
As shown in the diagram and photograph below, the sine-wave output of an oscillator is amplified and then sent through a small light bulb (GE44, 0.25 A at 6.3 V) and the A string of a violin. The purpose of the light bulb is to limit the current through the violin string. The gain of the amplifier is increased until the light bulb is at approximately normal brightness.
The neck of the violin is sitting in the field of a large magnetron magnet. The magnetic field produces a force on the current in the violin string. Since the current is oscillating, so is the force. The oscillating force causes the violin string to vibrate at the frequency of the oscillator. As we sweep through the frequencies, we hear resonances whenever we exite standing waves in the violin string. These occur at harmonics or multiples of 440 Hz (pitch of the A string).
Listen to a audio demo. The A string of the violin has been loosened a little so that its pitch is actually about 413 Hz (A-flat). We did this so that the dial on the oscillator could sweep through all eight harmonics.

